렌더링 파이프라인(5) - Rasterization
메시의 폴리곤을 픽셀로 매칭시키는 과정을 래스터라이제이션(Rasterization)이라고 한다
- Cliping ➡️ Perspective Division ➡️ Back-face culling ➡️ Viewport transform ➡️ Scan Conversion
1. Cliping

절두체 경계에 걸쳐져있는 오브젝트를 잘라내어 절두체 외부에 있는 부분은 출력을 안 하도록 처리한다.
- 1) 삼각형 은 view frustum 바깥쪽에 위치하므로 제거된다.
- 2) 삼각형 는 view frustum 안쪽에 위치하므로 그대로 둔다.
- 3) 삼각형 는 view frustum과 교차하므로, view frustum 바깥에 놓인 부분을 잘라내는 작업이 필요하다.
기존 vertex 일부가 제거되고, 새로운 vertex를 추가해서 새로운 primitive를 만든다.
2. 원근 나눗셈(perspective division)
- 나눗셈에 사용된 좌표는 로, 이는 camera space의 평면으로부터 해당 vertex까지의 수직 거리를 나타내는 양수값이다.
- camera로부터 멀리 떨어져 있는 정점은 projection transform 후 좌표가 크므로,
로 나누는 연산은 머리 떨어진 물체를 작게 만든다. ➡️ 원근법 구현
- 아래 예시에서 에 의해 변환된 vertex의 좌표는 가 된다.
projection transform을 camera space의 한 점 (x, y, z, 1)에 적용한 예시
3. 뒷면 제거(back-face culling),
정점 처리 과정에서 우리는 뷰 프러스텀의 외부에 있는 물체들을 제거하는 뷰 프러스텀 컬링을 수행했다. 또한 이전의 클리핑 단계에서도 시야에서 벗어나는 일부분들을 제거했다. 이제 파이프라인엔 시야 내의 물체들만 존재한다. 그러나 여전히 우리 눈에 들어오지 않는 부분들이 존재한다. 바로 물체의 앞면이 아닌 뒷면이다.
다음 그림에서 물체가 불투명하다고 가정할 때, 삼각형 t1은 카메라에게 보이지 않는다. 따라서 이러한 삼각형들을 그리지 않는다면 그만큼 렌더링 속도가 향상될 것이다. 이처럼 물체의 뒷면을 제거하는 작업을 뒷면 제거(back-face culling) 라 한다. 예를 들어 게임 캐릭터를 앞에서 바라 볼 때 뒷모습을 그릴 필요는 없다. (아래 그림은 카메라 공간이지만 이해를 돕기 위한 그림이며, 실제론 클립 공간에서 수행된다.)
- 가상 camera를 등지고 있는 polygon을 back-face라고 부른다.
이는 camera에 보이지 않으므로 제거될 것이다. - 반면, camera를 향하는 polygon은 front-face라고 부르는데,
이는 보존되어 rasterizer의 다음 단계로 넘어갈 것이다.

- 카메라(EYE)가 삼각형 normal이 가리키는 방향의 반대쪽에 존재한다면 이 삼각형은 back-face이다. ➡️
- 이를 구분하기 위해선 삼각형의 vertex와 camera를 연결하는 벡터가 필요하다.
이를 라 하고, 삼각형 normal 와 의 내적을 계산해서 판단한다.
뒷면 제거의 실제 구현
projection transform 이후에는 모든 가 축과 나란해진다. (단일한 투영선과 일치됨)
projectoin transform이 적용된 구가 주어졌을 때, 아래 예시처럼 이 구의 삼각형들을 단일한 투영선을 따라 평면으로 투영해보자.

3차원 공간에서는 을 포함한 모든 삼각형들의 vertex들이 반시계 방향으로 정렬되었었다.
그런데, back-face인 삼각형 을 투영한 결과는 vertex들이 시계 방향으로 정렬되어 있다.
반면, front-face인 삼각형 를 투영한 결과는 vertex들이 반시계 방향으로 정렬되어 있다.
이러한 성질을 이용해서,
2차원으로 투영된 vertex가 시계 방향으로 정렬되면 back-face로 판정하고,
반시계 방향으로 정렬되면 front-face로 판정한다.
삼각형의 vertex들이 시계 방향 혹은 반시계 방향으로 정렬되어 있는지는 행렬식(determinant)를 사용해 판정한다.
2차원으로 투영된 삼각형 를 생각해보자. 각 정정 는 좌표를 가진다.
우선 과 를 잇는 벡터 ,
그리고 과 를 잇는 벡터 을 계산한 후, 다음과 같은 행렬식을 이용한다.
이 행렬식의 값이 음수라면 시계방향, 즉 back-face이고
양수이면 반시계방향, 즉 front-face가 된다.
만약 0이라면, 변만 보이는 삼각형을 의미한다.
4. 뷰포트 변환(View-port transform)
우리들은 모니터의 스크린을 통해서 물체들을 보게 된다. 즉 물체들은 우리의 화면 상에 그려져야 한다. 그러나 프로그램에 따라 윈도우(창)의 크기는 다를 수 있다. 따라서 스크린 공간에 뷰포트라는 공간이 정의가 되며, 뷰포트는 그림이 그려지는 공간을 의미한다. 스크린과 뷰포트 공간은 3차원이며 모니터의 깊이를 z축이라 생각하면 된다. 깊이는 3차원 공간의 물체가 2D 화면에 그려질 때, 겹치는 물체의 우선순위를 판단하기 위한 수단으로 사용된다.뷰포트는 위와 같이 시작점 (MinX, MinY)와 너비(W)와 높이(H), 깊이 범위 [MinZ, MaxZ]로 정의된다. 물체가 항상 모니터라는 스크린 공간의 전체를 차지하는 것은 아니므로, 뷰포트의 시작점인 (MinX, MinY) 좌표는 유동적이다. (위 스크린 공간은 Direct3D 기준이다. OpenGL은 y축
이 반전되어 있다.)

Direct3D 기준으로 y축이 아래 방향으로 향하게 한다.


이러한 세 개의 변환 행렬의 곱을 하나의 행렬로 나타내면 다음과 같다.만약 뷰포트가 스크린의 일부분이 아닌 전체 영역을 차지할 경우 다음과 같이 간단하게 표현된다. MinX와 MinY는 모두 0이 되며, MinZ와 MaxZ는 0과 1이 된다.
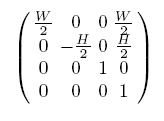

뷰 볼륨(뷰포트) 내의 물체를 뷰 볼륨 중앙으로 위치시킬 경우 위와 같이 이동 변환을 적용한다. 뷰포트의 시작점인 MinX,MinY에서 너비 및 높이의 반만큼 추가로 이동시킨 것이다. (Z축 방향으로의 이동은 잘 이해가 가지 않아 일단 보류해둠.)
3. 뷰 볼륨을 스크린 공간 내로 알맞게 이동시킨다.
기존의 뷰 볼륨은 너비, 높이, 깊이가 각각 2, 2, 1이었다. 이를 각각 W, H, MaxZ-MinZ로 만들기 위해 알맞은 수를 곱한다.
2. 뷰 볼륨의 너비를 W, 높이를 H, 깊이를 MaxZ-MinZ로 축소확대한다.
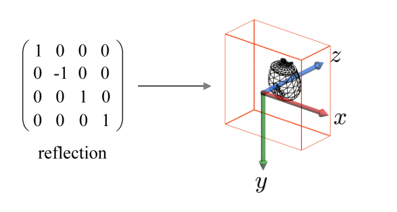
1. y축 반전
현재 우리의 물체들은 다음과 같은 정규화된 클립 공간인 NDC에 존재한다. 이를 위와 같은 뷰포트 공간으로 이동시키기 위해선 반사, 축소확대, 이동 3번의 변환이 필요하다.

5. 스캔 변환(Scan conversion)
래스터화의 마지막 단계인 스캔 변환은 스크린 공간의 물체들을 2차원 평면으로 나타내어, 물체를 구성하는 삼각형마다 프래그먼트로 채운다. 즉 모니터에 물체가 2차원 형태로 그려질텐데, 모니터 내의 모든 그림은 픽셀로 구성이 된다. 따라서 각 픽셀마다 위치가 정해져 있으며, 물체를 픽셀로 채워야 한다.아래와 같은 스크린 공간에서 우리는 모니터라는 2D 화면에 그리기 위해 (아직은) xy좌표만 고려한다. z좌표는 다른 단계에서 사용된다.정점은 위와 같이 다양한 속성을 가질 수 있다. 위와 같은 속성을 이용하여 프래그먼트를 생성할 수 있는데, 여기선 직관적이고 쉬운 예를 위해 컬러값 보간을 예로 든다.

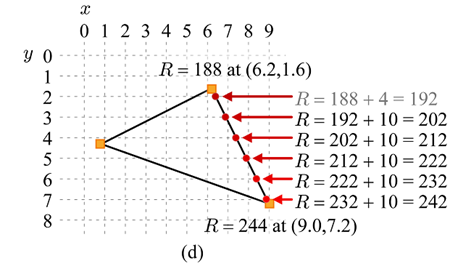
우선 1.6이라는 y값에서 7.2라는 y값이 되기 까지 R이 얼마나 증가하는지를 구해야 한다. 따라서 y증가량 = 7.2-1.6 = 5.6과 R의 증가량 = 244 - 188 = 56 이라는 값을 구한다. 그리고 R의 증가량을 y의 증가량으로 나눈다. 그러면 10이 나오는데, 이 의미는 y가 1증가할 때 R은 10 증가한다는 의미이다.
x증가량 = 6.9-3.4 = 3.5이며, 이때 R의 증가량 = 202-97 = 105 이다. 이를 통해 기울기를 구하면 30이고, xl = 3.4 지점부터 시작하여 R의 값을 구한다. 이 역시 계산을 쉽게 하기 위해 3.4가 아닌 4.0에서의 R값을 구한다. x가 1이 증가할 때 R이 30증가 하므로 x가 0.6증가하면 R은 18증가한다. 따라서 x가 4일 때 R의 값은 97+18 = 115이다. 이후부턴 x가 1증가할 때마다 y를 30씩 증가시켜주면 된다.

아래는 위와 같이 컬러가 보간된 삼각형의 예이다.
이처럼 정점을 이용하여 각 프래그먼트를 생성하는 것을 정점의 속성을 이용한 보간(interpolation)이라 한다. 처음엔 변을 따라 보간하고, 그 다음에는 스캔 라인을 따라 보간하였다. 이러한 두 단계를 거친 보간을 겹선형 보간이라고도 한다. 물론 이 예에선 단순한 이해를 위해 컬러값(R)만 보간하였다. 실제론 노멀, 텍스쳐 좌표, 깊이 등도 보간된다. 최종적인 컬러는 다음 단계에서 변경되거나 결정될 수 있다. 이처럼 래스터화의 마지막 단계인 스캔 변환은 정점별 속성을 보간하여 스캔 라인의 각 픽셀 위치마다 프래그먼트를 생성한다.

이제 삼각형 내의 모든 스캔 라인에 대한 R값을 구하기 위해, 아까와 같은 방식으로 x증가량에 대한 R의 증가량을 구한다. (삼각형 내의 픽셀(프래그먼트가) 생성될 각 라인을 스캔 라인이라 한다.)
첫 번째 정점의 y좌표는 1.6이고 R값은 188이다. 계산을 쉽게 하기 위해, 즉 증가 간격을 1로 잡기 위해 y가 2.0일 때의 R값을 구한다. y가 1증가할 때 R이 10 증가하므로, 0.4증가할 때 R은 4증가 한다. 따라서 y가 2.0일 때 R은 192이다. 이제부턴 y가 1씩 증가할 때 아래와 같이 R을 10씩 증가시켜주면 된다.

여기서 우리의 목표는 삼각형 내의 각 점마다 R값을 얻는 것이다. 이를 위해 R값을 가지고 있는 두 정점을 이용한다.
우선 아래와 같은 삼각형 내부에 프래그먼트를 생성한다고 생각해보자. 삼각형 내부에 컬러를 입히기 위해선 프래그먼트에 색상을 부여해서 생성해야 할 것이다. 그런데 삼각형 내부의 프래그먼트 하나하나를 위해 컬러값을 하나하나 저장해두는 것은 비효율적이다. 그래서 정점 속성의 컬러값으로 선형 보간을 하여서 정해진 기울기를 따라 자동으로 색상이 정해지도록 한다. 쉽게 말하면 기울기를 통해 규칙을 얻어 미리 컬러값의 증가량을 구하는 것이다. 그래서 정점에서의 하나의 컬러값으로 시작해 정해진 증가량에 따라 프래그먼트마다 컬러를 부여한다.

그러나 래스터화에선 프래그먼트라는 예비 픽셀로 먼저 채우게 된다. 프래그먼트는 각 정점이 가진 노멀, 텍스쳐 좌표, 색상 등과 같은 여러 정보를 이용하여 생성하게 된다. 즉 스캔 변환이란 2차원 평면에 그려질 물체들의 내부에 정점의 속성을 이용(보간)하여 프래그먼트를 생성하는 것을 말한다.